Answer: A: (6, 5)
Explanation:
When graphing a system of equations, you can find the solution by finding where the graphs intersect. In this case, the graphs intersect at (6, 5).
To verify that this is indeed a solution to the system of equations, we can substitute (6, 5) into both of the given equations:
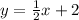
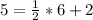
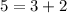
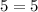
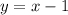
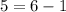
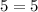
Since both equations hold true when plugging in the given coordinate (6, 5), we know that this is a solution to the system of equations.