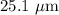Answer:
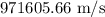
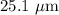
Step-by-step explanation:
m = Mass of electron =
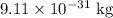
B = Magnetic field = 0.22 T
K = Kinetic energy of electron =
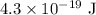
q = Charge =
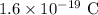
v = Velocity of electron
r = Radius of curved path
Kinetic energy is given by
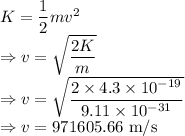
The speed of the electron is
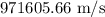
The force balance of the system is given by
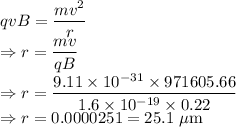
The radius of the curved path is