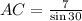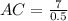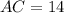Given the right triangle ABC with right angle B, angle A is twice the size of angle C. If the measure of side AB is 7 units, what is the measure of side AC?

Question

asked Sep 18, 2022 87.5k views

1 Answer

Janzell Jurilla · Answer 1 · 2022-09-24T11:02:41+0000

Answer:

AC= 14 units

Explanation:

Given

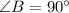$\angle B = 90^\circ$ --- right-angled

AB = 7

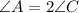
$\angle A = 2\angle C$

Required

Find AC

The question is illustrated using the attached triangle

The angles in a triangle are:

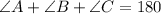
$\angle A + \angle B + \angle C = 180$

Substitute
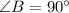$\angle B = 90^\circ$ and
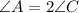
$\angle A = 2\angle C$

$2\angle C + 90 + \angle C = 180$

Collect like terms

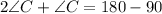
$2\angle C + \angle C = 180 - 90$

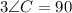
$3\angle C = 90$

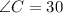
$\angle C = 30$

To find AC, we make use of the sine of angle C:

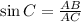$\sin C = (AB)/(AC)$ --- i.e. opposite/hypotenuse

So:

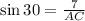
$\sin 30 = (7)/(AC)$

Make AC the subject

$AC= (7)/(\sin 30 )$

AC= (7)/(0.5)

AC= 14