Question

FIND THE AREA FOR BOTH SHAPES (LEAVE EXPLANATION)

Answer 1

b - 100 cm²

c - 45.5 cm²

Explanation:

Hello There!

For b - The following figure shown is a trapezoid with the dimensions

height = 10cm

longer base = 12cm

shorter base = 8cm

We can calculate the area of a trapezoid using this formula

`A=(a+b)/(2) h`

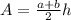
where a and b are bases and h = height

knowing the dimensions all we have to do is plug in the values

`A=(8+12)/(2) 10\\8+12=20\\(20)/(2) =10\\10*10=100`

so we can conclude that the area of figure b is 100 cm²

for a

The figure shown is an irregular shape so to calculate the area we're going to want to divide the irregular shape into two regular shapes

a rectangle with the dimensions:

width = 7 cm

length = 8cm (total height of irregular figure) - 3cm (height of the triangle)

8cm-3cm=5cm so the length of the rectangle is 5cm

a triangle with the dimensions:

base (length) = 7cm

height = 3cm

Now lets find the area of each shape

for the rectangle:

the area of a rectangle can simply be found by multiplying the length and width

7 * 5 = 35 so the area of the rectangle is 35 cm²

for the triangle:

the area of a triangle can be found using this formula

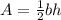`A=(1)/(2) bh` where b = base and h = height

knowing the dimensions all we have to do is plug in the values

`A=(1)/(2) 3*7\\3*7=21\\(21)/(2) =10.5`

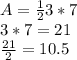
so we can conclude that the area of the triangle is 10.5 cm²

finally we add the two areas of the regular shapes

10.5 + 35 = 45.5 cm²

In conclusion the area of the figure is 45.5 cm²