Answer:
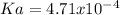
Step-by-step explanation:
Hello there!
In this case, according to the Henderson-Hasselbach equation, it is possible to write:
![pH=pKa+log(([A^-])/([HA]) )](https://img.qammunity.org/2022/formulas/chemistry/college/lcke64g1bi5g4xuc3x0kqs1orchgw6oe8m.png)
Next, since we are given the pH and the [A–]/[HA] ratio, we can solve for the pKa as shown below:
![pKa=pH-log(([A^-])/([HA]) )](https://img.qammunity.org/2022/formulas/chemistry/college/pyieeektsm1ywna5yeadisrmorfaf89r59.png)
Now, we plug in the values to obtain:
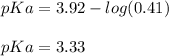
Next, Ka is:
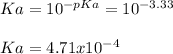
Best regards!