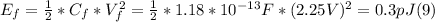Question

The plates of a vacuum-gap parallel plate capacitor have a 100.0 mm2 area, a vacuum gap of 5.00 mm and are connected to a 1.5-volt battery. After the capacitor is charged, the battery is disconnected from the capacitor. After the battery is disconnected, the plates are pulled apart until the vacuum gap is 7.50 mm. a. What are the initial and final energies stored in the capacitor

Answer 1

E₀ = 2.0*10⁻¹¹ J = 0.2 pJ

Ef = 3.0*10⁻¹¹ J = 0.3 pJ

Step-by-step explanation:

• The energy stored between the plates of a parallel plate capacitor can be expressed in terms of the capacitance C and the potential difference between plates V as follows:

`E = (1)/(2) * C * V^(2) (1)`

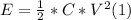
• When the capacitor is fully charged, the potential difference between plates must be equal to the voltage of the battery, 1.5 V.
• In a parallel plate capacitor, the value of the capacitance is independent of the applied voltage, and depends only on geometric constants and the dielectric constant of the medium between plates, as follows:

`C = (\epsilon_(o)*A)/(d) (2)`

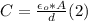
• We can find the initial value of C replacing in (2) by the givens below:
• A = 100.0 mm2
• d= 5.00 mm

• ε₀ = 8.85*10⁻¹² F/m
• 
  `C_(o) = (\epsilon_(o)*A)/(d) = ((8.85*(10)^(-12) F/m)*(10^(-4) m2))/(5.0*(10)^(-3)m) = 1.77*10^(-13) F (3)`
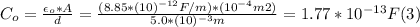
• With this value of C₀, and the value of the initial potential difference between plates (1.5 V), we can find the initial charge on the capacitor, starting from the definition of capacitance:
• 
  `C =(Q)/(V) (4)`
• Solving for Q in (4):
• 
  `Q = C_(o)* V = 1.77*10^(-13) F * 1.5 V = 2.65*10^(-13) C (5)`
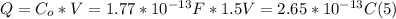
• Finally, we can find the initial energy stored in the capacitor, replacing (3) and V in (1):

`E_(o) = (1)/(2) * C_(o) * V_(o) ^(2) = (1)/(2) * 1.77*10^(-13)F*(1.5V)^(2) = 0.2 pJ (6)`

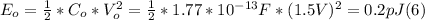
• If we pull apart the plates until the vacuum gap is 7.50 mm, we will change the expression of C in (2), decreasing its value due to the expanded gap.

• Replacing in (2) the new value of the gap (7.50 mm), we can find the new value of C, as follows:
• 
  `C = (\epsilon_(o)*A)/(d) = ((8.85*10^(-12)F/m)*10^(-4) m2)/(7.5*10^(-3)m) = 1.18*10^(-13) F (7)`
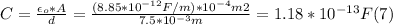
• In order to find the final energy stored in the capacitor, we need also the value of the final potential difference between plates.
• Once disconnected from the battery, the charge on any of the plates must remain the same, due to the principle of conservation of the charge.
• So, since we have the value of Q from (5) and the new value of C from (7), we can find the new potential difference between plates as follows:
• 
  `V_(f) = (Q)/(C_(f)) = (2.7*10^(-13)C)/(1.18*10^(-13)F) = 2.25 V (8)`
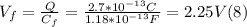
• With the values of Vf and Cf, we can find the value of the final energy stored in the capacitor, replacing these values in (1):

`E_(f) = (1)/(2) * C_(f) * V_(f) ^(2) = (1)/(2) * 1.18*10^(-13)F*(2.25V)^(2) = 0.3 pJ (9)`