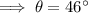Answer:

 = 46° (nearest degree)
= 46° (nearest degree)
Explanation:
In a right triangle, the hypotenuse is the longest side and the right angle is the angle opposite the hypotenuse.
From inspection of the diagram, and measuring and comparing the side lengths, it appears the that the longest side (hypotenuse) is "base" of the triangle (the side with an unknown measure), and so the right angle is the angle formed by the vertex of sides 22 and 21.
The trig ratio for sine is:
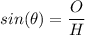
where
 is the angle, O is the side opposite the angle, and H is the hypotenuse.
is the angle, O is the side opposite the angle, and H is the hypotenuse.

At this stage, we don't know the measure of the hypotenuse. However, we can calculate it by using Pythagoras' Theorem
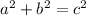 (where a and b are the legs, and c is the hypotenuse of a right triangle)
(where a and b are the legs, and c is the hypotenuse of a right triangle)


Therefore,