Question

Rewrite e^d=c in logarithmic form.
It says this is wrong, I'm not sure what I'm doing wrong

Answer 1

Explanation:

this is right.

but maybe your system wants you to use the special acronym for "logarithmus naturalis" (logarithm to the base of e) : ln

ln(c) = d

Answer 2

ln(c) = d

Explanation:

There are two types of logarithm:

• Common Logarithm
• Natural Logarithm

Common Logarithm is a logarithm with any base with real positive numbers other than e.

Here are some examples of what are common logarithm:

`\displaystyle \large{\log_3 9}\\\displaystyle \large{\log_{(1)/(2) 2}`

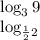
Natural Logarithm is a logarithm with a ‘e’ base only. You may notice that the answer you put in has a “e” base, that’s a natural logarithm.

It’s not wrong to answer as a
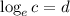`\displaystyle \large{\log_e c = d}` but the form is not commonly used. The natural logarithm has its own special form which is
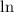`\displaystyle \large{\ln}`, the “ln” simply means the logarithm base e.

Here’s the comparison of writing ln and log base e:

`\displaystyle \large{\ln 2 = \log_e 2}\\\displaystyle \large{\ln 10 = \log_e 10}\\\displaystyle \large{\ln e = \log_e e \to 1}`

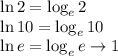
Therefore, your answer should be in “ln” form rather log base e.

Hence, the answer should be:
`\displaystyle \large{\ln (c) = d}`

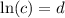
Hope this helps! Let me know if you have any questions.