Question

A stream of refrigerant-134a at 100 psia and 30°F is mixed with another stream at 100 psia and 80°F. If the mass flow rate of the cold stream is twice that of the hot one and the pressure is not changed, determine the enthalpy of the exit stream in Btu/lbm (with three significant figures).

Answer 1

The specific enthalpy of the exit stream is 63.267 Btu per pound-mass.

Step-by-step explanation:

This case represents a mixing chamber, a steady state device where two streams of the same fluid (cold and hot streams) are mixed with negigible changes in kinetic and gravitational potential energy and likewise in heat work interactions with surroundings. By Principle of Mass Conservation and First Law of Thermodynamics we have the following Mass and Energy Balances:

Mass Balance

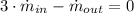`3\cdot \dot m_(in) - \dot m_(out) = 0` (1)

Where:

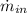`\dot m_(in)` - Mass flow of the hot stream, in pounds-mass per second.

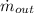`\dot m_(out)` - Mass flow of the resulting stream, in pounds-mass per second.

Energy Balance

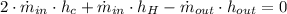`2\cdot \dot m_(in)\cdot h_(c)+\dot m_(in)\cdot h_(H)-\dot m_(out)\cdot h_(out) = 0` (2)

Where:

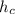`h_(c)` - Specific enthalpy of the cold stream, in BTU per pound-mass.

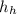`h_(h)` - Specific enthalpy of the hot stream, in BTU per pound-mass.

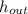`h_(out)` - Specific enthalpy of the resulting stream, in BTU per pound-mass.

By applying (1) in (2) we eliminate
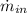`\dot m_(in)` and clear
`h_(h)`:

`h_(out) = (2\cdot h_(c)+h_(h))/(3)`

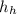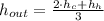
From Property Charts of the Refrigerant 134a, we have the following information:

Cold fluid (Subcooled liquid)

`p = 100\,psia`

`T = 30\,^(\circ)F`

`h_(c) \approx 37.870\,(Btu)/(lbm)`

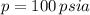
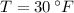
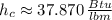
Hot fluid (Superheated steam)

`p = 100\,psia`

`T = 80\,^(\circ)F`

`h_(h) = 114.06\,(Btu)/(lbm)`

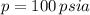
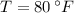
If we know that
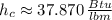`h_(c) \approx 37.870\,(Btu)/(lbm)` and
`h_(h) = 114.06\,(Btu)/(lbm)`, then the specific enthalpy of the resulting stream is:

`h_(out) = 63.267\,(Btu)/(lbm)`

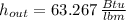
The specific enthalpy of the exit stream is 63.267 Btu per pound-mass.