Question

H2O enters a conical nozzle, operates at a steady state, at 2 MPa, 300 oC, with the inlet velocity 30 m/s and the mass flow rate is 50 kg/s. The exit pressure and temperature are 0.6 MPa and 160 oC, respectively. Please determine the inlet radius as well as the exit flow velocity. Hint: While the effect of heat transfer can be neglected, the change of the kinetic energy should be accounted for.

Answer 1

The flow velocity at outlet is approximately 37.823 meters per second.

The inlet radius of the nozzle is approximately 0.258 meters.

Step-by-step explanation:

A conical nozzle is a steady state device used to increase the velocity of a fluid at the expense of pressure. By First Law of Thermodynamics, we have the energy balance of the nozzle:

Energy Balance

`\dot m \cdot \left[\left(h_(in)+(v_(in)^(2))/(2) \right)-\left(h_(out)+(v_(out)^(2))/(2) \right)\right]= 0` (1)

Where:

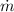`\dot m` - Mass flow, in kilograms per second.

`h_(in)`,
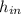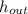`h_(out)` - Specific enthalpies at inlet and outlet, in kilojoules per second.

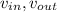`v_(in), v_(out)` - Flow speed at inlet and outlet, in meters per second.

It is recommended to use water in the form of superheated steam to avoid the appearing of corrosion issues on the nozzle. From Property Charts of water we find the missing specific enthalpies:

Inlet (Superheated steam)

`p = 2000\,kPa`

`T = 300\,^(\circ)C`

`h_(in) = 3024.2\,(kJ)/(kg)`

`\\u_(in) = 0.12551\,(m^(3))/(kg)`

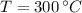
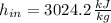
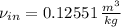
Where
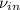`\\u_(in)` is the specific volume of water at inlet, in cubic meters per kilogram.

Outlet (Superheated steam)

`p = 600\,kPa`

`T = 160\,^(\circ)C`

`h_(out) = 2758.9\,(kJ)/(kg)`

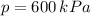
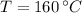
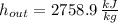
If we know that
`\dot m = 50\,(kJ)/(kg)`,
`h_(in) = 3024.2\,(kJ)/(kg)`,
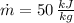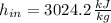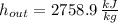`h_(out) = 2758.9\,(kJ)/(kg)` and
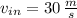`v_(in) = 30\,(m)/(s)`, then the flow speed at outlet is:

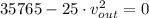`35765-25\cdot v_(out)^(2) = 0` (2)

`v_(out) \approx 37.823\,(m)/(s)`

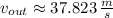
The flow velocity at outlet is approximately 37.823 meters per second.

The mass flow is related to the inlet radius (
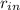`r_(in)`), in meters, by this expression:

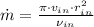`\dot m = (\pi \cdot v_(in)\cdot r_(in)^(2) )/(\\u_(in))` (3)

If we know that
`\dot m = 50\,(kJ)/(kg)`,
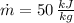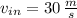`v_(in) = 30\,(m)/(s)` and
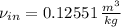`\\u_(in) = 0.12551\,(m^(3))/(kg)`, then the inlet radius is:

`r_(in) = \sqrt{(\dot m\cdot \\u_(in))/(\pi\cdot v_(in))}`

`r_(in)\approx 0.258\,m`

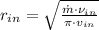
The inlet radius of the nozzle is approximately 0.258 meters.