Question

What is the value of x in the equation shown below?
x3 + 1 = 9

Answer 1

x = 7/3 or 2.33

Explanation:

x3 + 1 = 8

x3 = 8 - 1

x3 = 7

x = 7/3 or 2.33

HOPE THIS HELPS YOU!! :)

Answer 2

Answer: x = 2

Step 1.

In order to solve this non-linear equation, we need to move all the terms to the left side.

In x³ + 1 = 9...

- term 1, will be moved to the right side.

Notice that a term changes sign when it 'moves' from one side of the equation to the other.

Rewrite the equation like this: (x³ + 1) + (-1) = 9 + (-1)

Step 2.

Add x³ + 1 + (-1)

x³ + 1 + (-1) = 8

Now, x = 8.

Step 3.

In this non-linear equation, the variable needs to be isolated.

This is accomplished when both sides are exponentiated by the reciprocal of the variable's exponent, which in our example, 1/3 is equal to

Notice that since we exponentiated a simplified fraction with an odd denominator, only one solution has been created.

Rewrite the equation:
`(x^3)^(1)/(3) =8^(1)/(3)`

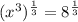
Step 4.

We need to exponentiate the power.

The following rule is applied:
`(A^B)^C=A^B^C`

According to the formula,

A = X

B = 3

C = 1/3

Rewrite the equation:
`x^3^*^(1)/(3) =(2^3)^(1)/(3)`

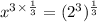
Step 5.

We need to reduce this fraction, the 3 in x to the lowest terms.

This can be done by dividing out those factors that appear both in the numerator and in the denominator.

In our example, 3 is the common factor.

Rewrite the equation:
`x=2^(3)/(3)`

Step 6.

Lastly, we'll need to do the same thing as we did in step 5. Reduce the fraction in
`x=2(3)/(3)`. This can be done by dividing out those factors that appear both in the numerator and in the denominator.

Hence, the common factor is 3 since it occurs both in the numerator and the denominator.

Hence, x = 2.