Answer:
a = 15
b = - 14
Explanation:
Solve the equation for a
a = 29 + b
Substitute the given value of a into the equation
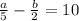

Solve the equation for b
b = - 14
Substitute the given value of b into the equation a = 29 + b
a = 29 + (- 14)
Solve the equation for a
a = 15
The possible solution of the system is the ordered pair (a, b)
(a, b) = (15, -14)
Check if the given ordered pair is the solution of the system of equations
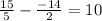
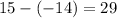
Simplify the equalities
10 = 10
29 = 29
Since all of the equalities are true, the ordered pair is the solution of the system
(a, b) = (15, -14)