Question

Lillian is going to invest in an account paying an interest rate of 5.7% compounded continuously. How much would Lillian need to invest, to the nearest ten dollars, for the value of the account to reach $7,600 in 7 years?

Answer 1

She has to invest $5,160 for the value of the account to reach $7,600 in 7 years.

Explanation:

Continuous compounding:

The amount of money earned, after t years, in continuous compounding, is given by:

`A(t) = A(0)(1+r)^t`

In which A(0) is the value of the initial investment and r is the interest rate, as a decimal.

Lillian is going to invest in an account paying an interest rate of 5.7% compounded continuously.

This means that
`r = 0.057`

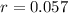
How much would Lillian need to invest, to the nearest ten dollars, for the value of the account to reach $7,600 in 7 years?

We have to find A(0) when
`A(t) = 7600, t = 7`

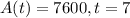
So

`A(t) = A(0)(1+r)^t`

`7600 = A(0)(1+0.057)^7`

`A(0) = (7600)/((1.057)^7)`

`A(0) = 5156`

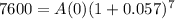
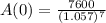
To the nearest ten dollars, she has to invest $5,160 for the value of the account to reach $7,600 in 7 years.