Question

if you apply the changes below to the linear parent function, f(x) = x, what is the equation of the new function?​

Answer 1

Answer: g(x)= -4x

Explanation:

Answer 2

Given:

The linear parent function is

`f(x)=x`

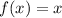
To find:

The new function after vertical stretch by a factor of 4 and flip over the x-axis.

Solution:

The transformation is defined as

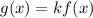`g(x)=kf(x)` .... (i)

Where, k is either vertical stretch or vertical compression.

If 0<|k|<1, then the graph compressed vertically by factor |k| and if |k|>1, then the graph stretch vertically by factor |k|.

If k<0, then the graph flip over the x-axis.

It is given that the graph of f(x) vertically stretch by a factor of 4. So, |k|=4.

The graph flip over the x-axis. So, the value of k must be negative, i.e., k=4.

Using (i), we get

`g(x)=-4f(x)`

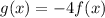
We have,
`f(x)=x`

`g(x)=-4x`

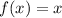
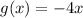
Therefore, the correct option is B.