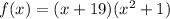Answer:
Explanation:
Complex numbers:
The following relation is important for complex numbers:
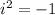
Zeros of a function:
Given a polynomial f(x), this polynomial has roots
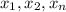 such that it can be written as:
such that it can be written as:
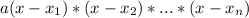 , in which a is the leading coefficient.
, in which a is the leading coefficient.
Has zeros −19 and −i
If -i is a zero, its conjugate i is also a zero. So
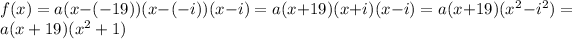
Output of 40 when x=1
This means that when
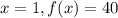 . We use this to find the leading coefficient a. So
. We use this to find the leading coefficient a. So
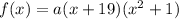
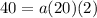
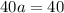
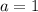
The polynomial is: