RIGHT TRIANGLE
Answer:
— — — — — — — — — —
We can find the length of the missing side of the right triangle using the Pythagorean Theorem.
As you can see in the attached image, we are looking for b or the longer side/leg of the right triangle. (See the attached image for the right triangle.)
Using the formula c² = a² + b².
we let c=12.21 and a=7
By transposition/adding the additive inverse of 49.
The difference of 149.0841 - 49 is 100.084
Hence, the measures of the longer side/leg is 10 units.
— — — — — — — — — —
We can also find the longer leg of the right triangle using the formula
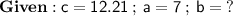
Substitute the given values of a and c to the given formula above, to get the unknown value (b).
_______________∞_______________