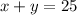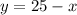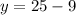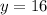Answer:
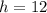
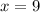
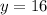
Explanation:
Given
The attached triangle
Required
Find h, x and y
Let the base of the triangle be 15.
So, the area is:
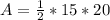

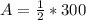

Let the base of the triangle be 25.
So, the area is:
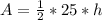
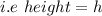

Substitute


Solve for h

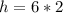
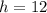
Considering the smallest triangle
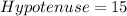
So:
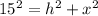
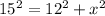
This gives:
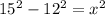
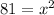
Take square roots
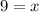
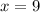
Solving for y