Answer:
Look below
Explanation:
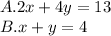
Either remove the x or y
Lets do X first
In order to remove the 2 from eqaution A, we need to make the coefficient be the same for the x in the equation B.
We can multiply eqaution B by 2 in order to have the same x coefficient as eqaution A. In addition, we must make the 2 a negative (-2) in order to remove x.
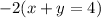
Now that we have the Xs ready for the elimination, we can proceed to answer for y
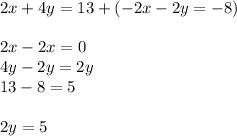
Now solve for y
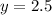
Now plug in 2.5 for either equation to find x ( in this case, B to make my life easier)
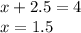
Which in order to trust the other equation ( for some people to trust the answer for X -_-)
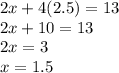
And from there, we conclude that x = 1.5 and y = 2.5
Now, we can get the same result if we eliminated y instead of x
(also this is copy and pasted from x because I am too lazy, get use to it)
In order to remove the 4 from eqaution A, we need to make the coefficient be the same for the y in the equation B.
We can multiply eqaution B by 4 in order to have the same x coefficient as eqaution A. In addition, we must make the 4 a negative (-4) in order to remove x.
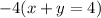
Now that we have the Ys ready for the elimination, we can proceed to answer for x
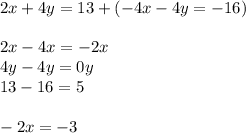
Now solve for x

Afterward, we are then able to do the same thing to find Y as we did previously in the previous section
Was this worth my time? No
Was it worth it? Yes
Why? I did this instead of a buddy's speech, so lol its funny to me lol