Answer:
Part A)
784 feet in the air (after five seconds).
Part B)
After 12 seconds.
Explanation:
The height h (in feet) of a rocket t seconds after being fired is modeled by the function:
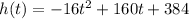
Part A)
We want to find the rocket's maximum height.
Since our function is a quadratic, the maximum height will occur at its vertex. The vertex of a quadratic is given by:
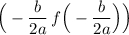
In this case, a = -16, b = 160, and c = 384.
So, the vertex occurs at:
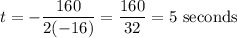
The maximum height is reached after five seconds.
Then the maximum height is:
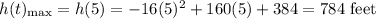
Part B)
When the rocket reaches the ground, its height h above the ground will be 0. Hence:
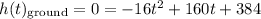
Solve for t. We can first divide both sides by -16:
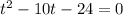
Factor:
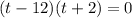
Zero Product Property:

Solve for each case:
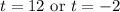
Time cannot be negative. Hence, our only solution is:
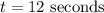
The rocket reaches the ground 12 seconds after it is fired.