Question

Akira is a salon owner. Yesterday, she did 2 haircuts and colored the hair of 1 client, charging a total of $194. Today, she did 2 haircuts and colored the hair of 4 clients, charging a total of $494. How much does Akira charge for her services?

Answer 1

`\boxed {\boxed {\sf Haircut: \$47 \ and \ Color: \$ 100}}`

Explanation:

Let's set up a system of equations. (1 equation for yesterday and 1 for today).

• Let h = haircut and c= color

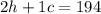`2h+1c= 194` (Yesterday: 2 haircuts and 1 color for $194).

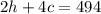`2h+4c= 494` (Today: 2 haircuts and 4 colors for $494).

Notice that both equations have a 2h. If we subtract the two equations, the 2h will cancel and leave us with one variable, c.

`\ \ (2h+1c=194) \\- (2h+4c=494)`

`\ \ 1c=194 \\- (4c=494)`

`-3c= -300`

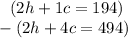
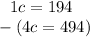
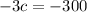
Since we are solving for c, we must isolate the variable. It is being multiplied by -3. The inverse of multiplication is division. Divide both sides by -3.

`-3c/-3=-300/-3 \\c= -300/-3 \\c=100`

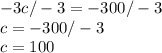
Now we have to solve for h. Plug 100 in for c in the first equation.

`2h+1(100)= 194 \\2h+100=194`

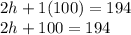
100 is being added, so we must subtract 100 from both sides.

`2h+100=194-100 \\2h=94`

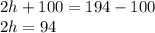
h is being multiplied by 2, so we divide both sides by 2.

`2h/2=94 \\h=47`

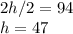
A haircut costs $47 and a color costs $100.