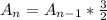Answer:
Explanation:
A recursive geometric formula has the pattern:
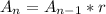where r is the common ratio. Before we write the formula, we need to find the value for r. This r value has to be the same between each consecutive number in the series. Because it's geometric, r is multiplied in (whereas it's added in if the sequence is arithmetic). To get from 1/2 to 3/4 we find the r value in this way:
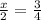where x/2 is the same as 1/2 x. Cross multiply to get 4x = 6 and x = 3/2. That means that if r is 3/2, then we can multiply every term in that sequence by 3/2 to get to the next term in line. 3/4 times 32 is 9/8. Therefore, r = 3/2 and the formula will be:
