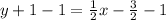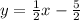Question

Which is an equation of the line that has a slope of 1/2 and passes through the point (3, -1)?

Answer 1

y + 1 = (1/2)(x - 3) - point-slope form

OR

y = (1/2)x - 5/2 - slope-intercept form

Explanation:

Given a slope and point, use point-slope form to write the equation for the line:

y - y1 = m(x - x1)

(x1, y1) is the point given and m is the slope.

y - (-1) = (1/2)(x - 3)

y + 1 = (1/2)(x - 3)

If you need to rewrite in slope intercept form, you can do so by distributing the 1/2 to the x - 3 and subtracting 1 from both sides:

y + 1 = (1/2)x - 3/2

y = (1/2)x - 5/2

Answer 2

`\boxed {\boxed {\sf y= \frac {1}{2}x - \frac {5}{2}}}`

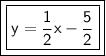
Explanation:

The equation of a line can be found using the point-slope formula.

`y-y_1=m(x-x_1)`

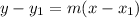
where m is the slope and (x₁, y₁) is the point the line passes through. For this line, the slope is 1/2 and the point is (3, -1). Therefore,

`m= \frac {1}{2} \\x_1= 3 \\y_1= -1`

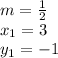
Substitute the values into the formula.

`y--1= \frac {1}{2}(x-3)`

`y+1= \frac {1}{2}(x-3)`

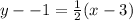
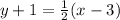
The equation can be left like this, or put into slope-intercept form (y=mx+b).

First, distribute the 1/2. Multiply each term inside the parentheses by 1/2.

`y+1= \frac {1}{2}x - \frac {3}{2}`

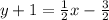
Next, subtract 1 from both sides of the equation.

`y+1-1= \frac {1}{2}x - \frac {3}{2}-1`

`y= \frac {1}{2}x - \frac {5}{2}`