Answer:
w =

(Anyone can correct me if I'm wrong)
Explanation:
Before we start the solving, we can make the following statements:
Area = l x w
Area = 5x + 25
therefore,
l x w = 5x + 25
Since the question states that the length is x more than the width, so we can make the following statement:
w = l + x
With this, we can substitute it to the first statement we made, l x w = 5x + 25,
l x (l + x) = 5x + 25
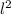 + lx = 5x + 25
+ lx = 5x + 25
lx - 5x = 25 -
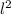
x(l - 5) = 25 -
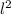
x =

From this, we can find w by substituting it in the statement we made earlier, w = l + x,
w =
