Question

Deduce the minimum value of sinx+cosx and give the corresponding values of x, for x E [-360;360]

Answer 1

The minimum value of both sine and cosine is -1. However the angles that produce the minimum values are different,
`-\pi/2, \pi` for sine and cosine respectively.

The question is, can we find an angle for which the sum of sine and cosine of such angle is less than the sum of values at any other angle.

Here is a procedure, first take a derivative

`(d)/(dx)(\sin x+\cos x)=\cos x -\sin x`

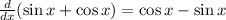
Then compute critical points of a derivative

`\cos x-\sin x=0\implies x_1=(\pi)/(4),x_2=(5\pi)/(4)`.

Then evaluate
`\sin x +\cos x` at
`x_1,x_2`.

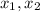You will obtain global maxima and global minima
`√(2), -√(2)` respectively.

The answer is
`-√(2)`.

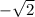Hope this helps.