Given:
Consider the below figure attaches with this question.
To find:
The size of angle x.
Solution:
Law of Cosines:
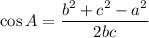
Three sides of the triangle are 11 cm, 8 cm, 15 cm. Since 11 cm is the opposite side of the angle x, therefore
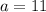 .
.
Let
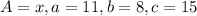 . Substitute these values in the above formula.
. Substitute these values in the above formula.
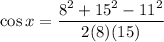
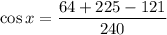
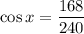
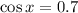
Taking cos inverse on both sides, we get
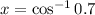
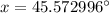
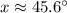
Therefore, the measure of angle x is 45.6°.