1 Answer

Chuk Lee · Answer 1 · 2022-07-22T16:31:13+0000

Given:

The inequality is

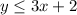
$y\leq 3x+2$

To find:

The ordered pair that is NOT a solution to the inequality in the graph.

Solution:

We have,

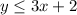
$y\leq 3x+2$

Checking the inequality for (0,0), we get

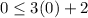
$0\leq 3(0)+2$

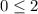
$0\leq 2$

So, the equality is true for (0,0). it means (0,0) is a solution of given inequality.

Checking the inequality for (-2,-4), we get

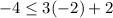
$-4\leq 3(-2)+2$

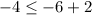
$-4\leq -6+2$

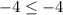
$-4\leq -4$

So, the equality is true for (-2,-4). It means (-2,4) is a solution of given inequality.

Checking the inequality for (0,2), we get

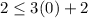
$2\leq 3(0)+2$

$2\leq 2$

So, the equality is true for (0,2). It means (0,2) is a solution of given inequality.

Checking the inequality for (-3,4), we get

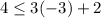
$4\leq 3(-3)+2$

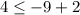
$4\leq -9+2$

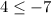
$4\leq -7$

This statement is not true. So, the equality is false for (-3,4). It means (-3,4) is not a solution of given inequality.

Therefore, the correct option is D.

Please log in or register to add a comment.