Question

A hoop is rotating at 12 rad/s on a horizontal plane about an a vertical axis that passes through its

edge when a second body with mass one quarter of the disc's is placed safely on it just opposite of the
pivot. What is the percentage change of the kinetic energy of the hoop?
A. 20%
B. 80%
C. 36%
D. 64%​

Answer 1

the correct answer is C

Step-by-step explanation:

For this exercise we can use the conservation of angular momentum, let's define a system formed by the disk and the other body, so that the torques during the collision have been internal and the moment is conserved.

Initial instant. Before placing the second body

L₀ = I₁ w₁

Final moment. Right after placing the body

L_f = (I₁ + I₂) w

the moment of inertia of the ring with respect to an axis passing through its center is tabulated

I_{cm} = m r²

we use the parallel axes theorem to find the moment of inertia about an axis passing through one end

I₁ = I_{cm} + m d²

where d is the distance from the center of mass to the new axis

d = r / 2

we substitute

I₁ = mr² + m (r/2)²

I₁ = 5/4 m r²

The second body does not specify a specific shape, so we can assume it to be punctual

I₂ = m’ (2r)²

I₂ = 4 m’ r²

in the exercise indicate that

m ’= m / 4

I₂ = m r²

how the moment of inertia is conserved

L₀ = L_f

I₁ w₁ = (I₁ + I₂) w

5/4 m r² w₁ = (5/4 m r² + m r²) w

5/4 m r² w₁ =9/4 m r² w

w = 5/9 w₁

we calculate

w = 5/9 12

w = 6.67 rad / s

having the initial and final angular velocities we can find the kinetic energy of the hoop

K₀ = ½ I₁ w₁²

K_f = ½ (I₁) w2

the energy ratio is

`(K_f)/(K_o)` =
`(w^2)/(w_1^2)`

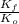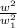
\frac{K_f}{K_o} = (6.67 / 12)²

\frac{K_f}{K_o} = 0.309

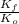`(K_f)/(K_o) %` = 31%

the correct answer is C