Convert y=x^2-4x+5 to vertex form by completing the square

Question

asked Jun 21, 2022 177k views

1 Answer

Laurent Sarrazin · Answer 1 · 2022-06-24T23:27:43+0000

Answer:

The vertex form will be:

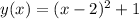
y(x)=(x-2)^(2)+1

Explanation:

The equation of the vertex form of a quadratic equation is given by:

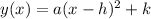
y(x)=a(x-h)^(2)+k

Where:

a is a coefficient

h is the x value of the vertex

k is the y value of the vertex

To completing the square we just need to add and subtract the square of the term with x divided by 2.

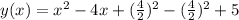
y(x)=x^(2)-4x+((4)/(2))^(2)-((4)/(2))^(2)+5

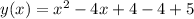
y(x)=x^(2)-4x+4-4+5

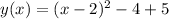
y(x)=(x-2)^(2)-4+5

Finally, the vertex form will be:

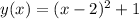
y(x)=(x-2)^(2)+1

I hope it helps you!