Given:
The vertices of a quadrilateral are v(-2,-1) w(-5,-2) x(-8,-7) and y(1,-6).
To find:
The vertices of the image of quadrilateral vwxy after 180° about the origin.
Solution:
If a figure rotated 180° about the origin, then the rule of rotation is
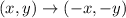
Using this rule, we get
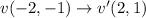
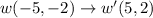
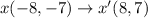
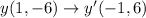
Therefore, the vertices of image of quadrilateral vwxy after 180° about the origin are v'(2,1), w'(5,2), x'(8,7), y'(-1,6).