Question

The certain forest moon travels in an approximately circular orbit of radius

14,441,566 m with a period of 6 days 10 hr, around its gas giant exoplanet host. Calculate the mass of the exoplanet from this
information. (Units: kilograms)

Answer 1

Mass of Exoplanet = 0.58 kg

Step-by-step explanation:

First, we will calculate the speed of the forest moon:

`speed = v = (Circumference)/(time)\\`

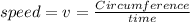
circumference = 2πr = 2π(14441566 m) = 90739035.3 m

time = 6 days 10 hr = (6 days)(24 h/1 day)(3600 s/1 h) + (10 h)(3600 s/1 h)

time = 554400 s

Therefore,

`v = (90739035.3\ m)/(554400\ s)\\\\v = 163.67\ m/s`

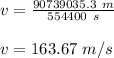
We know that the centripetal force on forest moon will be equal to the gravitational force given by Newton's Gravitational Law, as follows:

`Centripetal\ Force = Gravitational\ Force\\(m_(moon)v^2)/(r) = (Gm_(moon)m_(exoplanet))/(r^2)\\\\m_(exoplanet) = (v^2r)/(G)\\\\m_(exoplanet) = ((163.67\ m/s)^2(14441566))/(6.67\ x\ 10^(-11)\ N.m^2/kg^2)`

Mass of Exoplanet = 0.58 kg