Question

The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 5 minutes. Find the probability that a randomly selected passenger has a waiting time greater than 4.25 minutes. Find the probability that a randomly selected passenger has a waiting time greater than 4.25 minutes.

Answer 1

0.15 = 15% probability that a randomly selected passenger has a waiting time greater than 4.25 minutes.

Explanation:

A distribution is called uniform if each outcome has the same probability of happening.

The uniform distributon has two bounds, a and b, and the probability of finding a value higher than x is given by:

`P(X > x) = (b - x)/(b - a)`

Uniformly distributed between 0 and 5 minutes.

This means that
`a = 0, b = 5`

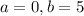
Find the probability that a randomly selected passenger has a waiting time greater than 4.25 minutes.

`P(X > 4.25) = (5 - 4.25)/(5 - 0) = 0.15`

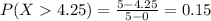
0.15 = 15% probability that a randomly selected passenger has a waiting time greater than 4.25 minutes.