Answer:
B = (10, -4), D = (58/9, -2)
Explanation:
Point C(3.6, -0.4) divides in the ratio 3 : 2. If the coordinates of A are (-6, 5), the coordinates of point B are ___ . If point D divides in the ratio 4 : 5, the coordinates of point D are ___ .
Solution:
If point O(x, y) divides line segment AB with endpoints at A(x₁, y₁) and B(x₂, y₂) in the ratio n:m, then:
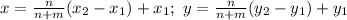
Since point C divides AB in the ratio 3:2. Let the coordinates of B be (x₂, y₂). Hence:
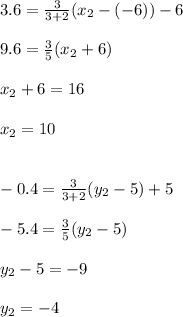
B = (10, -4)
D divides CB in the ratio 4:5. Let D = (x, y). Hence:
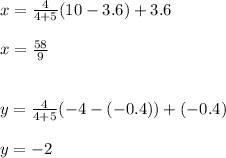
Hence D = (58/9, -2)