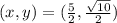Question:
Find the point (,) on the curve
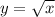 that is closest to the point (3,0).
that is closest to the point (3,0).
[To do this, first find the distance function between (,) and (3,0) and minimize it.]
Answer:
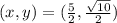
Explanation:
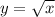 can be represented as:
can be represented as:

Substitute
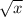 for
for

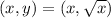
So, next:
Calculate the distance between
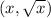 and
and
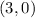
Distance is calculated as:
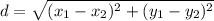
So:
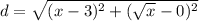
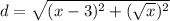
Evaluate all exponents
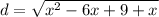
Rewrite as:
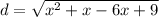
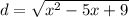
Differentiate using chain rule:
Let

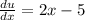
So:

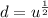
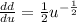
Chain Rule:
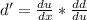
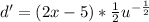
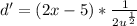
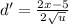
Substitute:

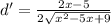
Next, is to minimize (by equating d' to 0)
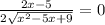
Cross Multiply
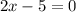
Solve for x
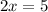
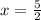
Substitute
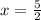 in
in
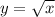
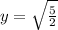
Split
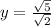
Rationalize
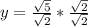
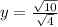

Hence: