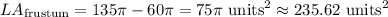Answer:
Part A)
The lower base has a radius of 9 units, and the upper base has a radius of 6 units.
Part B)
5 units.
Part C)
75π or about 235.62 square units.
Explanation:
Please refer to the figure below.
The cone has a radius of 9 units and a total height of 12 units.
A frustum of the cone has a height of 4 units.
Part A)
The lower radius of the frustum will simply be 9 units.
For the upper radius, we will use the properties of similar triangles. We will compare the smaller upper triangle to the overall larger triangle. This yields:
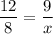
Solve for x. Simplify:
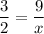
Cross-multiply:

The upper base has a radius of 6 units.
Part B)
We can first find the total slant height of the entire cone. By using the Pythagorean Theorem, this yields that the total slant height is:
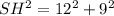
Simplify:
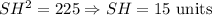
Now, find the slant height of the upper cone:
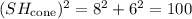
So:

Then the slant height of the frustum will be the cone subtracted from the total. Thus:

Part C)
We can first find the lateral area of the entire cone. The lateral area is given by:
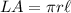
The lateral area of the entire cone will be:
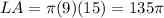
The lateral area of the upper cone will be:
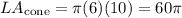
Then the lateral area of the frustum is: