Complete Question:
A tungsten wire is 1.5 m long and has a diameter of 1.0 mm. A current of 60 mA flows through the wire. The resistivity of the wire is 5.6 * 10^-8 Ωm. What is the potential difference across the ends of the wire?
Answer:
Potential difference, V = 0.00642 Volts.
Step-by-step explanation:
Given the following data;
Diameter = 1 mm to meters = 1/1000 = 0.001 m
Length = 1.5m
Current = 60mA = 60/1000 = 0.06 Amperes.
Resistivity = 5.6 * 10^-8 Ωm
To find the potential difference across the ends of the wire;
First of all, we would determine the cross-sectional area of the wire (circle);
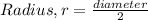
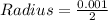
Radius = 0.0005 m
Area of wire (circle) = πr²
Substituting into the above formula, we have;
Area = 3.142 × (0.0005)²
Area = 3.142 × 2.5 × 10^-7
Area = 7.855 × 10^-7 m²
Next, we find the resistance of wire;
Mathematically, resistance is given by the formula;
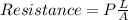
Where;
P is the resistivity of the material.
L is the length of the material.
A is the cross-sectional area of the material.
Substituting into the formula, we have;
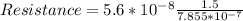
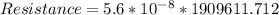
Resistance = 0.107 Ohms.
Now, we can find the potential difference using the formula;
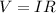
Where;
V represents voltage or potential difference measured in volts.
I represents current measured in amperes.
R represents resistance measured in ohms.
Substituting into the formula, we have;

Potential difference, V = 0.00642 Volts.