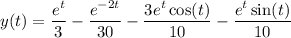Question

Problem 3: Use the Laplace Transforms to solve:


`y'' + y - 2y= {e}^( t) sin(t), \\ y(0) =y'(0) =0`
​

Answer 1

Using the transforms listed in your attachment and taking the Laplace transform of both sides of the ODE gives

`L\{y''+y'-2y\} = L\{e^t \sin(t)\}`

`(s^2 Y(s) - s y(0) - y'(0)) + (s Y(s) - y(0)) - 2 Y(s) = L\{e^t \sin(t)\}`

`(s^2 + s - 2) Y(s) = L\{e^t \sin(t)\}`

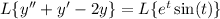
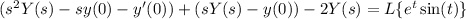
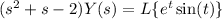
where Y(s) denote the Laplace transform of y(t).

For the remaining transform, we use the frequency shifting property,

`L\left\{e^(at) f(t)\right\} = F(s - a)`

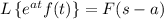
Then

`L\{\sin(t)\} = F(s) = \frac1{s^2+1} \\ \implies L\left\{e^t\sin(t)\right\} = F(s - a) = \frac1{(s - 1)^2+1} = \frac1{s^2-2s+2}`

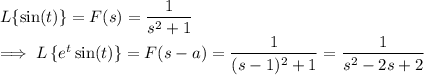
Solving for Y(s) yields

`Y(s) = \frac1{(s^2-2s+2)(s^2+s-2)} = \frac1{(s - 1)(s + 2) (s^2 - 2s + 2)}`

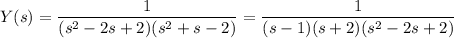
Break up the right side into partial fractions.

`\frac1{(s - 1)(s + 2) (s^2 - 2s + 2)} = \frac a{s-1} + \frac b{s+2} + (cs + d)/(s^2 - 2s + 2)`

`\frac1{(s - 1)(s + 2) (s^2 - 2s + 2)} =\\ (a(s+2)(s^2-2s+2) + b(s-1)(s^2-2s+2)+(cs+d)(s-1)(s+2)))/((s - 1)(s + 2) (s^2 - 2s + 2))`

`1 = a(s+2)(s^2-2s+2) + b(s-1)(s^2-2s+2)+(cs+d)(s-1)(s+2)`

`1 = 4 a - 2 b + 2 d + (-2 a + 4 b + 2 c - 2 d) s + (-3 b - 2 c + d) s^2 + (a + b + c) s^3`

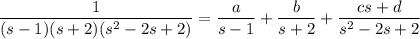
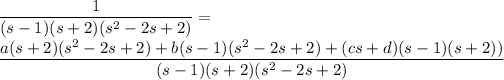
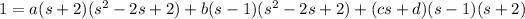
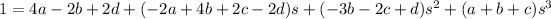
Solve for the unknown coefficients:

`\begin{cases}4a-2b+2d=1 \\ -2a+4b+2c-2d = 0 \\ -3b-2c+d = 0 \\ a+b+c=0\end{cases} \implies a=\frac13,b=-\frac1{30},c=-\frac3{10},d=\frac15`

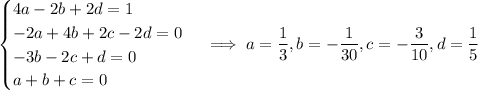
So we have

`Y(s) = \frac13*\frac1{s-1} -\frac1{30}* \frac1{s+2} - \frac3{10} * (s)/(s^2-2s+2) + \frac15 *\frac1{s^2-2s+2}`

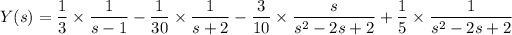
which we can rewrite as

`Y(s) = \frac13*\frac1{s-1} -\frac1{30}* \frac1{s+2} - \frac3{10} * (s - 1)/((s-1)^2+1) - \frac1{10} *\frac1{(s-1)^2+1}`

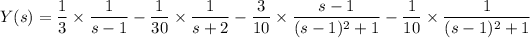
Now use the frequency-shifting property to compute the inverse transforms.

`L^(-1)\left\{\frac1{s-1}\right\} = e^t L^(-1)\left\{\frac1s\right\} = e^t`

`L^(-1)\left\{\frac1{s+2}\right\} = e^(-2t) L^(-1)\left\{\frac1s\right\} = e^(-2t)`

`L^(-1)\left\{(s-1)/((s-1)^2+1)\right\} = e^t L^(-1)\left\{\frac s{s^2+1}\right\} = e^t\cos(t)`

`L^(-1)\left\{\frac1{(s-1)^2+1}\right\} = e^t L^(-1)\left\{\frac1{s^2+1}\right\} = e^t\sin(t)`

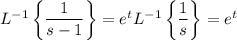
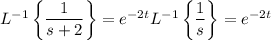
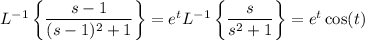
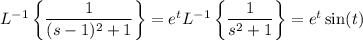
Putting everything together, we end up with

`y(t) = \frac{e^t}3 - (e^(-2t))/(30) - (3e^t\cos(t))/(10) - (e^t\sin(t))/(10)`