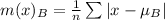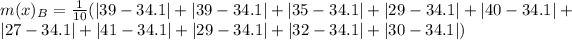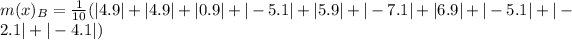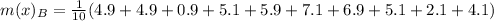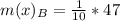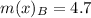Answer:
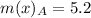 --- Mean absolute deviation of educational documentary
--- Mean absolute deviation of educational documentary
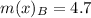 --- Mean absolute deviation of prime time drama
--- Mean absolute deviation of prime time drama
Explanation:
Given

See attachment for table
Required
Determine the mean absolute deviation of each
Mean absolute deviation m(x) is calculated as:

For Educational Documentary
First, calculate the mean
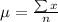
So:
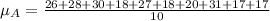


The mean absolute deviation is then calculated as:
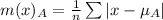
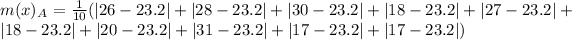
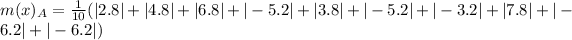
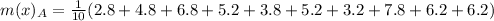
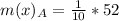
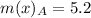
For Prime time Drama
First, calculate the mean
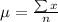
So:
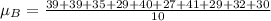
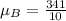
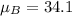
The mean absolute deviation is then calculated as: