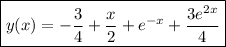Question

Problem 2: Use the Laplace Transforms to solve:


`y'' - y' - 2y= 1 - x , \\ y(0) =y'(0) =1`
​

Answer 1

Using the given table of transforms,

`L\left\{ y'' - y' - 2y \right\} = L\left\{ 1-x \right\}`

`(s^2 Y(s) - sy(0) - y'(0)) - (s Y(s) - y(0)) - 2 Y(s) = \frac1s - \frac1{s^2}`

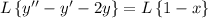
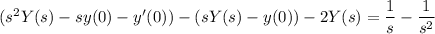
(where Y(s) is the Laplace transform of y(x))

Solve for Y(s) :

`(s^2 - s - 2) Y(s) - s = \frac1s - \frac1{s^2}`

`(s^2 - s - 2) Y(s) - s = (s-1)/(s^2)`

`(s^2 - s - 2) Y(s) = (s-1)/(s^2) + s`

`(s^2 - s - 2) Y(s) = (s^3 + s - 1)/(s^2)`

`Y(s) = (s^3 + s - 1)/(s^2 (s^2 - s - 2))`

`Y(s) = (s^3 + s - 1)/(s^2 (s + 1) (s - 2))`

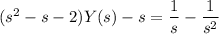
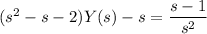
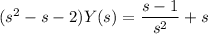
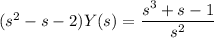
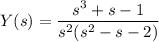
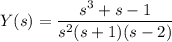
Decompose the right side into partial fractions:

`Y(s) = \frac as + \frac b{s^2} + \frac c{s+1} + \frac d{s-2}`

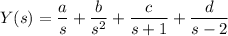
Solve for the coefficients.

`\implies s^3 + s - 1 = as(s+1)(s-2) + b(s+1)(s-2) + cs^2(s-2) + ds^2(s+1)`

`\implies s^3 + s - 1 = -2 b + (-2 a - b) s + (-a + b - 2 c + d) s^2 + (a + c + d) s^3`

`\implies \begin{cases}-2b = -1 \\ -2a-b = 1 \\ -a+b-2c+d = 0 \\ a+c+d = 1 \end{cases} \implies a=-\frac34, b=\frac12, c=1, d=\frac34`

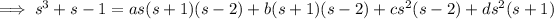
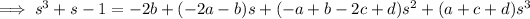
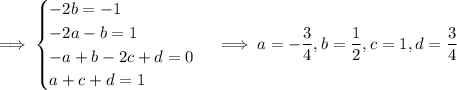
Then

`Y(s) = -\frac34 * \frac1s + \frac12 * \frac1{s^2} + \frac1{s+1} + \frac34 *\frac1{s-2}`

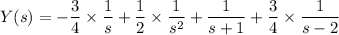
Take the inverse transform and solve for y(x) :

`F(s) = \frac1s \implies f(x) = 1`

`F(s) = \frac1{s^2} \implies f(x) = x`

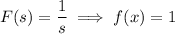
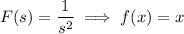
Using the frequency-shifting property,

`F(s) = \frac1{s+1} \implies f(x) = e^(-x)`

`F(s) = \frac1{s-2} \implies f(x) = e^(2x)`

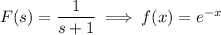
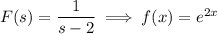
So, the particular solution to the ODE is

`\boxed{y(x) = -\frac34 + \frac x2 + e^(-x) + \frac{3e^(2x)}4}`