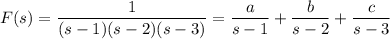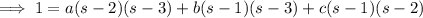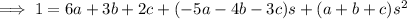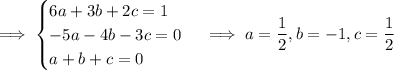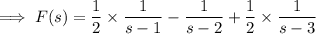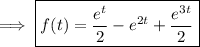Question

Problem 0: Compute the inverse Laplace Transforms of:


`F(s) = (s + 1)/(s(s - 1)(s - 3))`


`F(s) = (1)/((s - 1)(s - 2)(s - 3))`

​

Answer 1

Decompose each given F(s) into partial fractions.

`F(s) = (s+1)/(s(s-1)(s-3))`

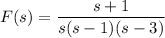
has partial fraction decomposition

`(s+1)/(s(s-1)(s-3)) = \frac as + \frac b{s-1} + \frac c{s-3}`

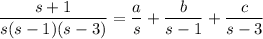
Combine the rational terms on the right and solve for the coefficients:

`(s+1)/(s(s-1)(s-3)) = (a(s-1)(s-3) + b s(s-3) + c s(s-1))/(s (s-1) (s-3))`

`1 = a(s-1)(s-3) + bs(s-3) + c s(s-1)`

`1 = 3 a + (-4 a - 3 b - c) s + (a + b + c) s^2`

`\begin{cases}3a=1 \\ -4a-3b-c = 0 \\ a+b+c=0 \end{cases} \implies a=\frac13, b=-\frac12, c=\frac16`

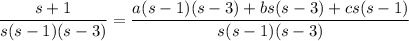
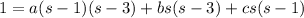
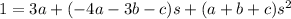
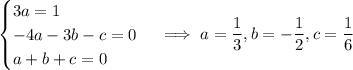
Then

`F(s) = \frac13 * \frac1s - \frac12 * \frac1{s-1} + \frac16 * \frac1{s-3}`

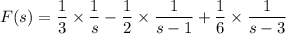
Using the frequency-shifting property, the inverse transform is

`\boxed{f(t) = \frac13 - \frac{e^t}2 + \frac{e^(3t)}6}`

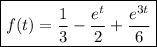
The other transform can be dealt with in the same manner.

`F(s) = \frac1{(s-1)(s-2)(s-3)} = \frac a{s-1} + \frac b{s-2} + \frac c{s-3}`

`\implies 1 = a(s-2)(s-3) + b(s-1)(s-3) + c(s-1)(s-2)`

`\implies 1 = 6 a + 3 b + 2 c + (-5 a - 4 b - 3 c) s + (a + b + c) s^2`

`\implies \begin{cases}6 a + 3 b + 2 c=1 \\ -5a-4b-3c = 0 \\ a+b+c=0\end{cases} \implies a=\frac12, b=-1, c=\frac12`

`\implies F(s) = \frac12 * \frac1{s-1} - \frac1{s-2} + \frac12 * \frac1{s-3}`

`\implies \boxed{f(t) = \frac{e^t}2 - e^(2t) + \frac{e^(3t)}2}`