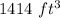Answer: 14
Explanation:
Given
Excavation cone measures
height
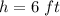
Diameter
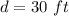
Truck can dump
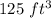 at a time
at a time
The volume of a cone is
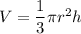
Putting values
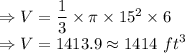
No of trips(N) required to accumulate this much volume is given by
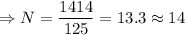
Therefore, 14 trips are necessary to accumulate a cone of volume