Answer:
Vf = 69.61 m/s
Step-by-step explanation:
We will use the third equation of motion to solve this problem:
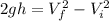
where,
g = acceleration due to gravity = 9.81 m/s²
h = height of cliff = 247 m
Vf = final velocity = ?
Vi = initial velocity = 0 m/s (boulder breaks loose from rest)
Therefore,
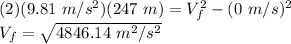
Vf = 69.61 m/s