Question

Solve the equation. (Find all solutions of the equation in the interval [0, 2pi). Enter your answers as a comma-separated list.)

(3 sin(2x) + 3 cos(2x))^2=9

Answer 1

I got

`0.75 + 2\pi * n`

`5.28 + 2\pi * n`

`1 + 2\pi * n`

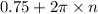
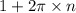
5.53+2pi times n

WORK:

`(3 \sin(2x) + 3 \cos(2x) )) {}^(2) = 9`

`\sin(2x) + \cos(2x) {}^(2) = 3`

`\sin(x) + \cos(4 {x}^(2) ) = 3`

`4 {x}^(2) + x = 3`

`4 {x}^(2) + x - 3 = 0`

`(4x {}^(2) + 4x - 3x - 3 = 0`

`4x(x + 1) - 3(x + 1) = 0`

`(4x - 3)(x + 1)`

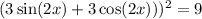
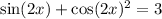
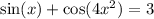
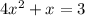
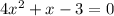
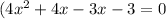
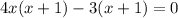
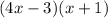
Solve for x

`4x - 3 = 0`

`4x = 3`

`x = (3)/(4)`

`x + 1 = 0`

`x = - 1`

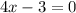
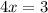
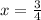
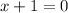
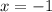
While -1 is a solution, it isn't within the interval of 0,2pi.

However, we can use the reference angle identity

`\cos(x) = \cos(x + 2\pi)`

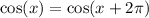
So some more possible points are

`- 1 + 2\pi`

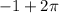
Since it on a interval, it must be less than 2 pi or 6.28.

Let find some more points

`- 1 + 2\pi = 5.28`

So 5.28 is a point,

`(3)/(4) + 2\pi = 7.03`

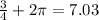
That is too big since -6.28 is smaller than 7.03

We can use the identity

`\cos(x) = \cos( - x)`

`\cos( - 1) = \cos( 1 )`

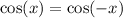
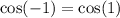
1 is smaller than 2pi so it is true.

`\cos( (3)/(4) ) = \cos( - (3)/(4) )`

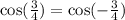
Negative 3/4 is smaller than zero so it not a solution.

`0.75`

`5.28`

`1`

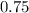
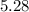
Make sure to include

`2\pi * n`

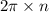
so

`0.75 + 2\pi * n`

`5.28 + 2\pi * n`

`1 + 2\pi * n`

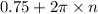
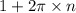
We can also -3/4 plus 2 pi.

Which is about 6

5.53.