Question

Write and solve an inequality to find the values of x for which the perimeter of the rectangle is less than 140.

Select the correct answer below and fill in the answer box to complete your choice.
PLZ HELP MEEE

Answer 1

Given:

Length of the rectangle =
`x+4`

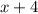
Width of the rectangle =
`x`

The perimeter of the rectangle is less than 140.

To find:

The inequality for the given situation and solve it.

Solution:

We have,

`l=x+4`

`w=x`

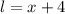
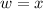
We know that, the perimeter of a rectangle is

`P=2(l+w)`

`P=2(x+4+x)`

`P=2(2x+4)`

`P=4x+8`

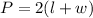
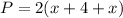
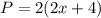
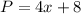
It is given that the perimeter of the rectangle is less than 140.

`P<140`

`4x+8<140`

`4x<140-8`

`4x<132`

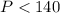
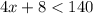
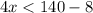
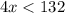
Divide both sides by 4.

`x<(132)/(4)`

`x<33`

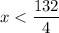
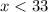
Therefore, the correct option is A because the sign of inequality is < and the solution of inequality is
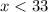`x<33`.