Answer:

Explanation:
The sides of a right triangle can be found using Pythagorean Theorem.

where a and b are legs and c is the hypotenuse.
In this triangle, the legs are 15 and 7, so we can substitute those values in for a and b.
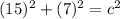
Solve the exponents.
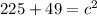
Add.
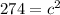
Since we are solving c, we have to isolate the variable. It is being squared and the inverse of a square is a square root. Take the square root of both sides.

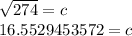
Let's round to the nearest hundredth. The 2 in the thousandth place tells us to leave the 5.
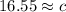
The hypotenuse is approximately √274 or 16.55 inches