Question

A help desk has two employees with one working during the day and one working at night. The number of hours the first employee works (X1) is normally distributed with mean 8.6 and standard deviation 0.1 and the number of hours the second employee works (X2) is normally distributed with mean 8.4 and standard deviation 0.9. Suppose that the amount of time that the employees overlap (X3) is normally distributed with mean 0.2 and standard deviation 0.2. Finally, assume that X1, X2, and X3 are independent. We are interested in the total time that the help desk has an employee present, i.e., Z = X1 + X2 - X3. A) What is the expected value of Z, the total time that the help desk has an employee present? B) What is the variance of Z? C) What is the probability that Z is between 15.9 and 16.1? D) What is the probability that Z is greater than 16?

Answer 1

a) 16.8 hours.

b) 0.86 hours squared.

c) 0.0606 = 6.06% probability that Z is between 15.9 and 16.1.

d) 0.8051 = 80.51% probability that Z is greater than 16

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Sum of normal variables:

When we add normal variables, the mean is the sum of each mean, while the variance is the sum of each variance. The standard deviation is the squared root of the variance.

In this question:

X1: Mean 8.6, standard deviation 0.1

X2: Mean 8.4, standard deviation 0.9

X3: Mean 0.2, standard deviation 0.2

Z = X1 + X2 - X3.

Mean:

`\mu = 8.6 + 8.4 - 0.2 = 16.8`

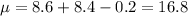
Variance:

`\sigma^(2) = 0.1^2 + 0.9^2 + 0.2^2 = 0.86`

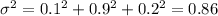
Standard deviation:

`\sigma = \sqrt{\sigma^(2)} = √(0.86) = 0.9274`

A) What is the expected value of Z, the total time that the help desk has an employee present?

`\mu = 16.8`

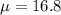
So 16.8 hours.

B) What is the variance of Z?

`\sigma = 0.86`

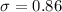
So 0.86 hours squared.

C) What is the probability that Z is between 15.9 and 16.1?

This is the pvalue of Z when X = 16.1 subtracted by the pvalue of Z when X = 15.9. So

X = 16.1

`Z = (X - \mu)/(\sigma)`

`Z = (16.1 - 16.8)/(0.9274)`

`Z = -0.75`

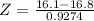
`Z = -0.75` has a pvalue of 0.2266

X = 15.9

`Z = (X - \mu)/(\sigma)`

`Z = (15.9 - 16.8)/(0.9274)`

`Z = -0.97`

`Z = -0.97` has a pvalue of 0.1660

0.2266 - 0.1660 = 0.0606

0.0606 = 6.06% probability that Z is between 15.9 and 16.1.

D) What is the probability that Z is greater than 16?

This is 1 subtracted by the pvalue of Z when X = 16. So

`Z = (X - \mu)/(\sigma)`

`Z = (16 - 16.8)/(0.9274)`

`Z = -0.86`

`Z = -0.86` has a pvalue of 0.1949

1 - 0.1949 = 0.8051

0.8051 = 80.51% probability that Z is greater than 16