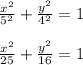Question

Write an equation for an ellipse centered at the orgin, which has foci ( plus minus 3, 0) and co-vertices at (0, plus minus 4)

Answer 1

The answer is below

Explanation:

The co-vertices of an ellipse are the endpoints of the minor axis. The equation for an ellipse is given by:

`((x-h)^2)/(a^2) +((y-k)^2)/(b^2)=1`

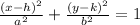
Where (h, k) is the center of the ellipse, (h, k±b) is the co-vertices, (h ± a, k) is the vertices, (h ± c, k) is the foci and c² = a² - b²

Since the center is the origin, hence (h, k) = (0, 0). i.e h = 0, k = 0.

Foci = (h ± c, k) = (± c, 0) = (±3, 0). c = 3

co-vertices = (h, k±b) = (0, ±b) = (0, ±4). b = 4

c² = a² - b²

a² = c² + b²

a² = 3² + 4² = 25

a = 5

Therefore the equation of the ellipse is:

`(x^2)/(5^2) +(y^2)/(4^2)=1 \\\\(x^2)/(25) +(y^2)/(16)=1`