Question

The desperate contestants on a TV survival show are very hungry. The only food they can see is some fruit hanging on a branch high in a tree. Fortunately, they have a spring they can use to launch a rock. The spring constant is 900 N/m, and they can compress the spring a maximum of 45 cm. All the rocks on the island seem to have a mass of 500 g.

a) With what speed does the rock leave the spring?
b) To what height can the rock be launched?

Answer 1

a) v = 18.86 m / s, b) h = 8.85 m

Step-by-step explanation:

a) For this exercise we can use the conservation of energy relations.

Starting point. Like the compressed spring

Em₀ = K_e + U = ½ k x² + m g x

the zero of the datum is placed at the point of the uncompressed spring

Final point. With the spring if compress

Em_f = K = ½ m v²

how energy is conserved

Em₀ = Em_f

½ k x² + m g x = ½ m v²

v² =
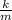`(k)/(m)` x² + 2gx

let's reduce the magnitudes to the SI system

m = 500 g = 0.500 kg

x = -45 cm = -0.45 m

the negative sign is because the distance in below zero of the reference frame

let's calculate

v² =
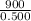`(900)/(0.500)` 0.45² + 2 9.8 (- 0.45)

v = √355.68

v = 18.86 m / s

b) For this part we use the conservation of energy with the same initial point and as an end point at the point where the rock stops

Em_f = U = m g h

Em₀ = Em_f

½ k x²2 + m g x = m g h

h = ½
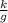`(k)/(g)` x² + x

let's calculate

h =
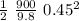`(1)/(2) \ (900)/(9.8 ) \ 0.45^2` - 0.45

h = 8.85 m

measured from the point where the spring is uncompressed