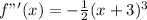Question is incomplete
Answer:
See Explanation
Explanation:
Let the cubic function be
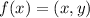
First transformation: Vertical compression
Let the scale factor be a where

The new function becomes:

Next: Reflection over y-axis
The rule is:
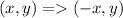
The new function becomes:
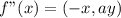
Lastly: Shifted up
Let the units up be b
The rule is:
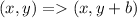
So, the new function becomes:
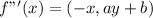
Using the rules states above, assume the cubic function is:
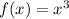
Vertical compress
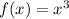 by
by

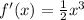
Reflect
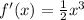 over y-axis
over y-axis
Rule:
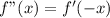
Solving f'(-x)
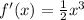
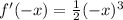

So:
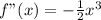
Lastly: Shift
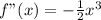 by 3
by 3
Rule:
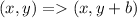

Solving: f"(x + 3)
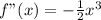
Substitute x + 3 for x
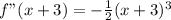
So: