Answer:
a. 0.1681 = 16.81% probability that all five qualify for the favorable rate.
b. 0.5283 = 52.83% probability that at least four qualify for the favorable rates
Explanation:
For each Puerto Rico resident, there are only two possible outcomes. Either they qualify for discounted rates, or they do not. The probability of a person in the sample qualifying for discounted rates is independent of any other person in the sample. This means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
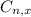 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
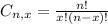
And p is the probability of X happening.
70% of the island residents of Puerto Rico have reduced their electricity usage sufficiently to qualify for discounted rates.
This means that
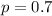
Five residential subscribers are randomly selected from San Juan, Puerto Rico
This means that
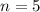
a. All five qualify for the favorable rate
This is P(X = 5). So

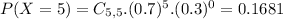
0.1681 = 16.81% probability that all five qualify for the favorable rate.
b. At least four qualify for the favorable rates
This is
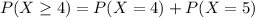
So

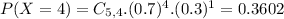
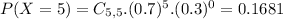
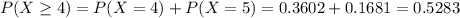
0.5283 = 52.83% probability that at least four qualify for the favorable rates