Question

Marvin invested 65% of his retirement account in stocks and 35% in gold. Marvin believes that the return to stocks over the next 12 months is normally distributed with mean rate of return of 10% and standard deviation of return of 15%. He also believes that the return to gold over the next 12 months is normally distributed with mean rate of return of 30% and standard deviation of return of 40%. Finally, Marvin believes that the return to stocks and the return to gold are independent.1. According to Marvin's beliefs, what are the mean rate of return and the standard deviation of return to his investment portfolio? 2. What is the probability that Marvin's portfolio will make at least 20% over the next 12 months? Show your work and explain. Write all the steps of your analysis and/or calculations so that it is clear how you reached your results.

Answer 1

1)

the mean rate of return is 17 %

the standard deviation of return is 17.06055

2)

the probability that Marvin's portfolio will make at least 20% over the next 12 months is 0.4325

Explanation:

Given the data in the question;

1)

For the portfolio, the mean return and standard deviation are computed as follows;

Mean = Return = 0.65 × 10 + 0.35 × 30

= 6.5 + 10.5

= 17 %

Therefore, the mean rate of return is 17 %

Standard deviation will be;

σp = √( 0.65² × 15² + 0.35² × 40² )

= √( 0.4225 × 225 + 0.1225 × 1600 )

= √( 95.0625 + 196 )

= √291.0625

= 17.06055

Therefore, the standard deviation of return is 17.06055

2)

probability that Marvin's portfolio will make at least 20% over the next 12 months.

P( X > 20 )

we convert to a standard normal variable;

Z =
`(20-17)/(17.06055)` )

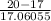Z = 0.17

from z table, p-value is;

p( X < 20 ) = 0.5675

P( X > 20 ) 1 - 0.5675 = 0.4325

Therefore, the probability that Marvin's portfolio will make at least 20% over the next 12 months is 0.4325